感知机算法的收敛性
对于线性可分的数据集,感知机学习算法的原始形式是收敛的。也就是说,经过有限次的迭代,可以找到一个将数据集完全正确划分的分离超平面。
本文是 <统计学习方法> 第二章感知机收敛性证明的笔记,主要加入了一点自己的理解。
在证明之前,先定义下相关的符号标记。
- 将参数 b 并入权重向量 w,记作
- 将输入向量加进常数 1,记作
很显然,向量内积
收敛性证明
Novikoff 定理
式 (2.8) 证明
由于训练数据集是线性可分的,存在超平面将训练数据集完全正确分开,取此超平面为
使
因此可以从所有样本中找到一个最小取值,使得
样本中所有数据均满足
式 (2.9) 证明
感知机算法中,如果实例被误分类,则更新权重。令
则对于第 k 个误分类实例,它的误分类判断条件为
若
即
下面推导两个不等式
其中第二步用到了式 (2.8)
其中第一步用到了
结合不等式 (2.12) 和 (2.13) 可得
首先看下第一个不等式,其中第一步就是 (2.12),第二步用到了施瓦茨不等式,第三步用到了 (2.13) 和证明一的条件
再看第二个不等式,对第一个不等式两侧取平方可得
因此可得
参考
李航。统计学习方法
- 2018-08-04
感知机算法是 <统计学习方法> 这本书讲的第一个机器学习算法,据说是最简单的机器学习算法。这里参考书中的例子,使用程序实现该算法,以便加深理解。
- 2018-07-19
本节首先介绍函数间隔和几何间隔的概念,进而引出最优间隔分类器和拉格朗日对偶,最后介绍核函数和 SMO algorithm
- 2018-07-08
前两节分别介绍了一个回归模型和一个分类模型,其中线性回归中假设概率分布为
- 2018-07-14
前面讲到的学习算法都是对
- 2018-07-07
二分类 (binary classification) 是最简单的一种分类问题,

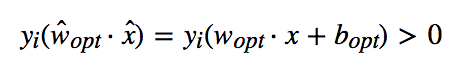
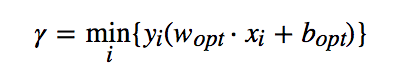
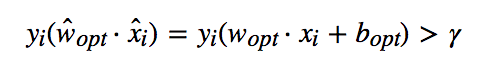
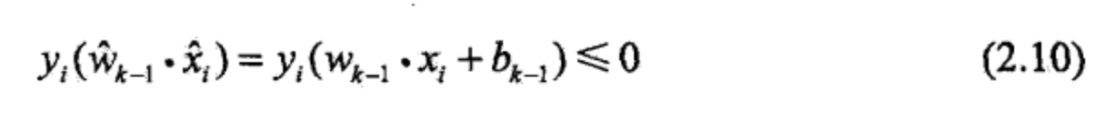

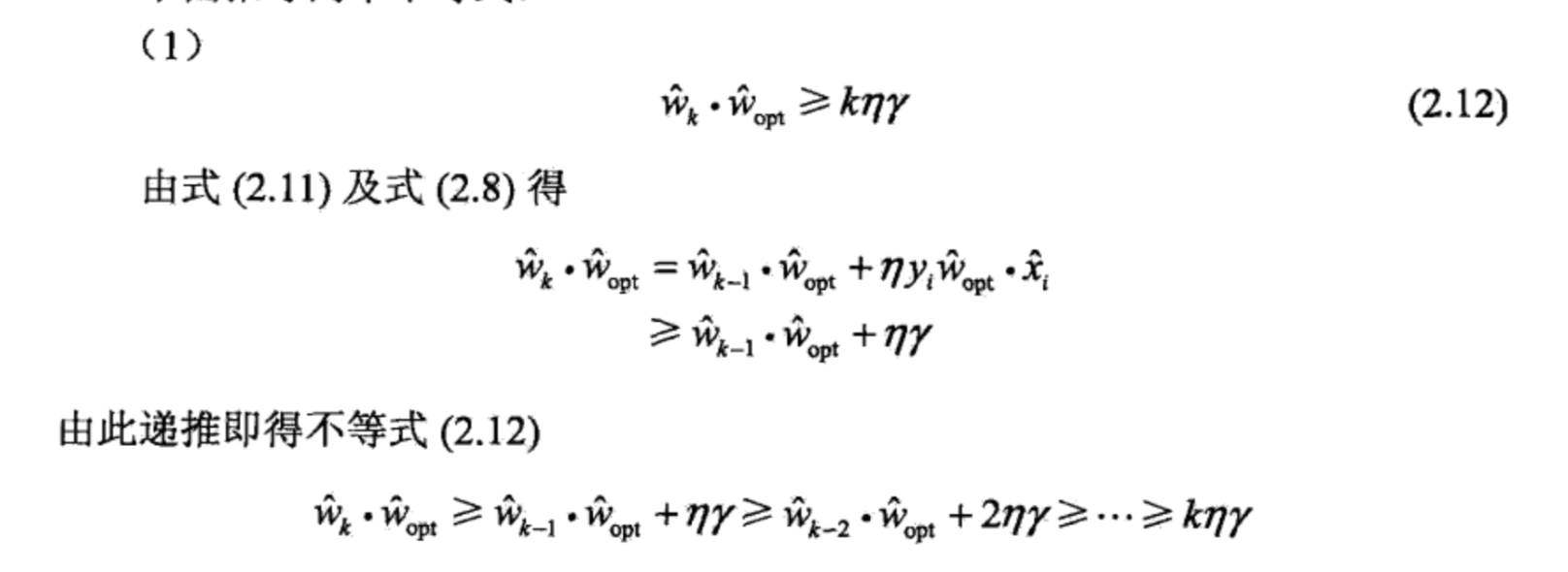
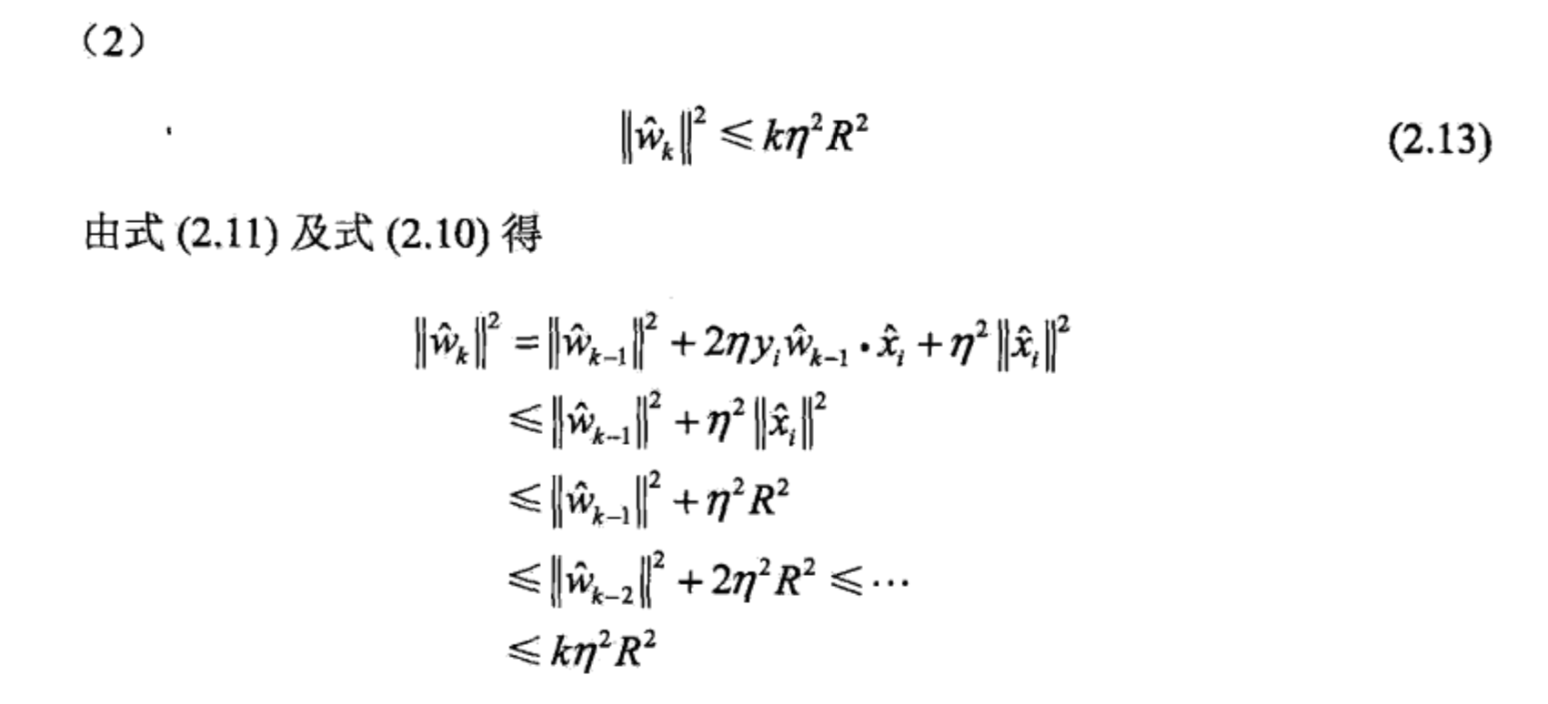
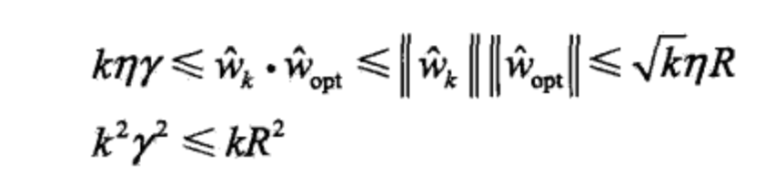
预览: