俗话说好记性不如烂笔头，看过的东西很快就会忘了，记录下来一方面会增强记忆，另一方面也方便查阅。这里根据css229视频和讲义简单做下笔记。

监督学习

本节定义了一些符号。$x^{(i)}$ 表示输入变量，也可以叫做特征。$y^{(i)}$ 表示输出变量，也可以叫做目标变量。$(x^{(i)}, y^{(i)})$ 表示一个训练样本，上标中的 (**i) **表示这是第 i 个样本。因此，对于一个包含 m 个训练样本的训练集，可以表示为如下形式

$${(x^{(i)}, y^{(i)}); i = 1,…,m}$$

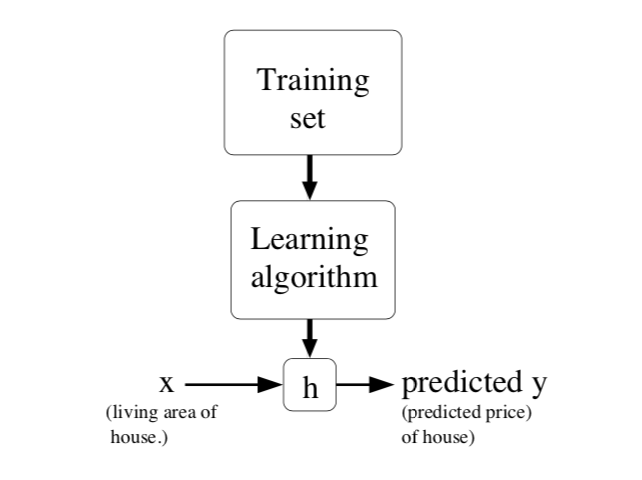
所谓监督学习，可以简单描述为：给定一个训练集，通过训练学习到函数 $h(x)$，使得它能够对新的输入 $x$ 得到 “好的” 预测结果 $y$。这里的 $h(x)$ 叫做 hypothesis

若预测结果是连续的，把这种学习问题称为 回归问题。若预测结果只有少数几个值，则称为 分类问题。

线性回归

对于监督学习，首先要考虑的是 hypothesis 的形式，线性回归自然用到的是线性函数。例如预测房价问题，$x$ 是二维向量，其中$x_1^{(i)}$ 表示第 i 个样本的房间面积，$x_2^{(i)}$ 表示第 i 个样本的卧室数量，则 $h(x)$ 可表示为如下形式

$$h_\theta(x) = \theta_0 + \theta_1x_1 + \theta_2x_2$$

其中 $\theta$ 是参数，又叫做权重，它通过线性函数将输入空间 $X$ 映射到输出空间 $Y$。为方便表示，可引入常量 $x_0 = 1$

$$h(x) = \sum_{i=0}^{n}\theta_ix_i = \theta^Tx$$

这里 $\theta$ 和 $x$ 均为向量，准确来说是列向量，$\theta^T$ 则是对应的行向量，根据向量乘法将上述公式展开可得到第一个公式

如何求 $\theta$ 的值呢？我们的目标是使得预测值尽可能接近实际值，也就是让预测值和实际值之间的距离 $|h_\theta(x) - y|$ 尽可能小，为了方便计算可对其取平方从而去掉绝对值符号，得到 $(h_\theta(x^{(i)}) - y^{(i)})^2$。考虑训练集中所有样本，对结果求和。通常为方便计算将上述值除以2，最终得到如下 损失函数

$$J(\theta) = \frac{1}{2}\sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})^2$$

LMS算法

为了最小化 $J(\theta)$，考虑 **梯度下降 **算法。所谓梯度，其实质是向量，表示函数在该点处的方向导数沿此方向取最大值。梯度下降可以理解为沿梯度的相反方向移动，使得函数值逐渐减小，这样最终可以找到一组参数值，使得函数值取最小值或接近最小值。对于每一个参数 $\theta_j$，可通过求偏导数 $\frac{\partial}{\partial \theta_j}J(\theta)$ 得到其梯度，进而可得到如下更新规则

$$\theta_j := \theta_j - \alpha\frac{\partial}{\partial \theta_j}J(\theta)$$

其中 $\alpha$ 称为 学习速率，它决定了函数值减小的速度。速率设置较大下降的速度会比较快，但也可能错过最小值；速率设置较小可能会需要比较多的迭代次数下降到最小值

\begin{align}
\frac{\partial}{\partial \theta_j}J(\theta)
&= \frac{\partial}{\partial \theta_j} \frac{1}{2} (h_\theta(x) - y)^2 \\
&= 2 \frac{1}{2} (h_\theta(x) - y) \frac{\partial}{\partial \theta_j} (h_\theta(x) - y) \\
&= (h_\theta(x) - y) \frac{\partial}{\partial \theta_j} (\sum_{i=0}^{n} \theta_i x_i - y) \\
&= (h_\theta(x) - y)x_j
\end{align}

只考虑一个样本，更新规则如下

$$
\theta_j := \theta_j + \alpha (y^{(i)} - h_\theta(x^{(i)})) x_j^{(i)}
$$

此更新规则叫做 **LMS **(least mean squares)更新规则，或 Widrow-Hoff learning rule。其中 $(y^{(i)} - h_\theta(x^{(i)}))$ 称为误差项。该规则可以理解为：如果预测值 $h_\theta(x^{(i)})$ 接近实际值 $y^{(i)}$，则仅需要对参数做较小的更新，否则需要较大的更新

稍作修改可应用于整个训练集。对于每一个参数 $\theta_j$，均需要使用 m 个样本数据进行计算。此方法称为 **批梯度下降 **法(batch gradient descent)

$$
\theta_j := \theta_j + \alpha \sum_{i=1}^{m}(y^{(i)} - h_\theta(x^{(i)})) x_j^{(i)}
$$

批梯度下降每次迭代需要对样本集中的所有样本进行计算，当样本集比较大时，计算量也会相应的变得比较大，甚至难以实现。此时可使用 **随机梯度下降 **(stochastic gradient descent)，每次迭代随机选取一个样本进行训练。使用随机梯度下降可以快速收敛到接近最小值，通常是在最小值附近波动。当样本集非常大时通常选用随机梯度下降法

概率解释

为什么选用 least-squares 损失函数作为线性回归的损失函数？实际上，在做出几个概率假设的条件下，可以很容易推导出该损失函数

假设输出变量和输入变量之间的关系可以用如下公式表示

$$
y^{(i)} = \theta^T x^{(i)} + \epsilon^{(i)}
$$

其中 $\epsilon^{(i)}$ 表示误差项。假定它符合独立同分布，即 IID(independently and identically distributed)，进一步假设其服从高斯分布(正态分布)，即 $\epsilon^{(i)} \sim N(0, \sigma^2)$，则它的概率密度可表示为

$$
p(\epsilon^{(i)}) = \frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(\epsilon^{(i)})^2}{2\sigma^2})
$$

可以得到

$$
p(y^{(i)}|x^{(i)};\theta) = \frac{1}{\sqrt{2\pi}\sigma} exp(- \frac{(y^{(i)} - \theta^Tx^{(i)})^2}{2\sigma^2})
$$

其中 $p(y^{(i)}|x^{(i)};\theta)$ 表示在条件 $x^{(i)}$ 下 $y^{(i)}$ 的概率分布，它以 $\theta$ 为参数，注意公式里面是分号

似然函数 likelihood function

$$
L(\theta) = L(\theta; X, \vec{y}) = p(\vec{y}|X; \theta)
$$

根据独立同分布假设

$$
\begin{align}
L(\theta) &= \prod_{i=1}^{m}p(y^{(i)} | x^{(i)}; \theta) \\
&= \prod_{i=1}^{m} \frac{1}{\sqrt{2\pi}\sigma} exp(- \frac{(y^{(i)} - \theta^Tx^{(i)})^2}{2\sigma^2})
\end{align}
$$

根据最大似然法，求出使 $L(\theta)$ 最大化时的 $\theta$。为方便计算，可改为使对数似然函数最大化

$$
\begin{align}
l(\theta) &= logL(\theta) \\
&= log\prod_{i=1}^{m} \frac{1}{\sqrt{2\pi}\sigma} exp(- \frac{(y^{(i)} - \theta^Tx^{(i)})^2}{2\sigma^2}) \\
&= \sum_{i=1}^{m}log \frac{1}{\sqrt{2\pi}\sigma} exp(- \frac{(y^{(i)} - \theta^Tx^{(i)})^2}{2\sigma^2}) \\
&= m \cdot log \frac{1}{\sqrt{2\pi}\sigma} - \frac{1}{\sigma^2} \cdot \frac{1}{2} \sum_{i=1}^{m} (y^{(i)} - \theta^Tx^{(i)})^2
\end{align}
$$

若要使其最大化，只需要使第二项最小化，也就是使下式最小化。这就是 $J(\theta)$，即最小二乘损失函数(least-squares cost function)。需要注意的是， $\theta$ 的取值不依赖于 $\sigma^2$，更进一步，即使 $\sigma^2$ 是未知的我们也可以得到相同的结果

$$
\frac{1}{2} \sum_{i=1}^{m} (y^{(i)} - \theta^Tx^{(i)})^2
$$

局部加权线性回归

在原始的线性回归算法中，我们的目标是找到 $\theta$ 的取值，使得 $\sum(y^{(i)} - \theta^Tx^{(i)})^2$ 最小化。

LWR(Locally weighted linear regression)算法中，目标是使如下式子最小化

$$
\sum w^{(i)}(y^{(i)} - \theta^Tx^{(i)})^2
$$

其中 $w^{(i)}$ 是非负的，叫做权重。如果它的取值比较小，则误差项对结果的影响也会比较小，否则会有较大影响。一个比较通用的权重公式是

$$
w^{(i)} = exp(- \frac{(x^{(i)} - x)^2}{2\tau ^2})
$$

这里权重的大小依赖于 $x$ 的选择，如果 $|x^{(i)} - x|$ 的值非常小，那么权重 $w^{(i)}$ 的取值就接近 $1$，否则权重的值就非常小(接近0)。注意 $w^{(i)}$ 不是随机变量

参数 $\tau$ 叫做 bandwidth 参数，可以理解为有效值的范围，超出一定范围后误差项对结果的影响大小下降的很快

LWR是非参数化学习算法。所谓参数化(parametric)学习算法，即训练出算法的参数后，可以使用算法对新的输入进行结果预测，不需要保留训练集，比如原始的线性回归算法。非参数化(non-parametric)学习算法刚好相反，需始终保留训练集