cs229 笔记 5:支持向量机
本节首先介绍函数间隔和几何间隔的概念,进而引出最优间隔分类器和拉格朗日对偶,最后介绍核函数和 SMO algorithm
直观解释
逻辑回归算法中,使用
考虑正样本的情况 (y=1)。
也就是说如果
对于给定的训练集,如果能够找到一个分界线,使得当
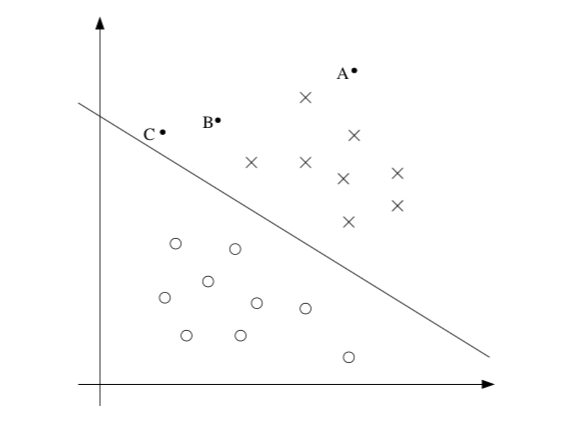
下图中 x 表示正样本,o 表示负样本,分界线为
很明显对于 A 的预测结果应为 y=1,而对于 C,预测结果也应为 y=1,由于它离分界线很近,稍微移动就会是结果变为 y=0,直观上认为 A 的预测结果可信度比 C 更高,B 则介于两者之间
符号表示
同样是二分类问题,考虑线性分类器,与之前不同的是,这里
其中当
函数间隔和几何间隔
给定训练集
当
对于函数间隔的参数,如果将
给定训练集 S = {
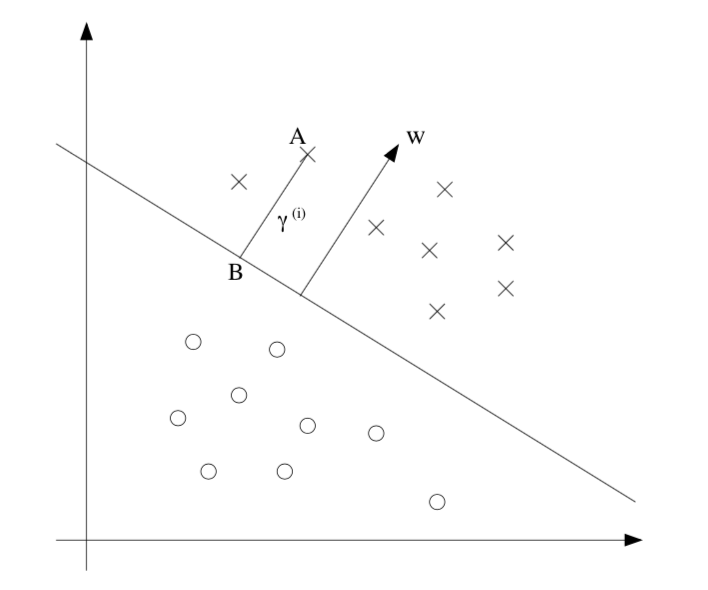
下面讨论几何间隔,首先看下图
图中展示了决策边界、向量 w (和决策边界垂直)。A 点表示一个输入为
求解
这表示的是正样本的情况。更一般地,几何间隔定义如下
注意如果
最优间隔分类器
根据之前的讨论,一个很自然的想法是最大化几何间隔,这样可以对训练集进行很好地分类。
假定训练集是线性可分的,也就是说可以用超平面对正样本和负样本进行划分。如何找到这个使得几何间隔最大化的超平面呢?给出如下最优化问题
我们的目标是最大化
因为条件
我们最大化的目标变成了
根据前面的讨论,我们可以随意等比例缩放 w、b 而不影响最终分类结果。这里考虑通过缩放使函数间隔满足
问题变为最大化
这是一个仅包含线性限制的凸二次最优化问题,可以很容易解决。这就是最优间隔分类器。
拉格朗日对偶
拉格朗日乘子法
考虑如下问题
定义拉格朗日函数
这里
原始问题
考虑如下原始最优化问题
它的广义拉格朗日函数为
对于它的最大值 (其中
如果 w 违反了任何原始限制 (比如
相反,如果满足限制则
原始问题的值
对偶问题
另一个问题,定义
其中下标
很容易证明,这两种问题之间的关系如下 (先取 max 再取 min 的值总是大于等于先取 min 再取 max 的值),并且在特定条件下两者相等
KKT 条件
KKT 条件是拉格朗日乘子法的推广。如果只包含等式约束条件,可以用拉格朗日乘子法求解最优值。如果约束条件中还包含不等式约束,则可以用 KKT 条件求解。
假设: 1. f 和 g 是凸函数 2. h 是仿射函数 3. 存在 w 使得对于所有的 i 均满足
仿射函数
仿射函数是特殊的凸函数,它是线性函数和常数之和
最优间隔分类器
回忆如下原始问题
可以把约束条件写为如下形式
补充
点到平面的距离
平面的表示
平面的常用表示方法有点法式、一般式和截距式。
假设
因为法向量垂直于平面上任意的向量,所以
这就是平面的点法式方程。替换常量,得到平面的一般式方程如下
向量的投影长度
向量
点到平面距离
点 (x,y,z) 为平面外一点,则它到平面的距离如下
其中
- 2018-07-07
二分类 (binary classification) 是最简单的一种分类问题,
- 2018-07-05
俗话说好记性不如烂笔头,看过的东西很快就会忘了,记录下来一方面会增强记忆,另一方面也方便查阅。这里根据 css229 视频和讲义简单做下笔记。
- 2018-07-08
前两节分别介绍了一个回归模型和一个分类模型,其中线性回归中假设概率分布为
- 2018-08-04
感知机算法是 <统计学习方法> 这本书讲的第一个机器学习算法,据说是最简单的机器学习算法。这里参考书中的例子,使用程序实现该算法,以便加深理解。
- 2018-08-05
对于线性可分的数据集,感知机学习算法的原始形式是收敛的。也就是说,经过有限次的迭代,可以找到一个将数据集完全正确划分的分离超平面。
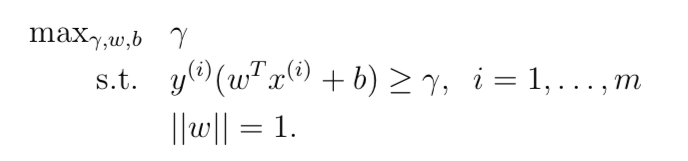
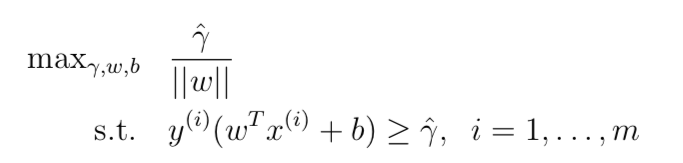
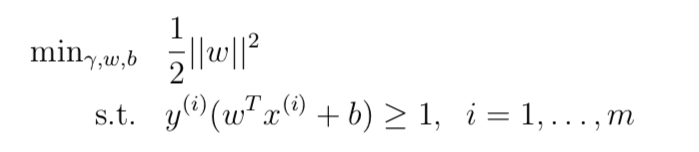
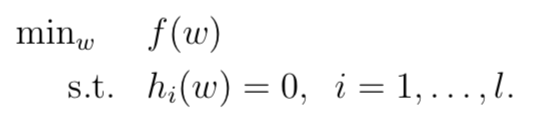
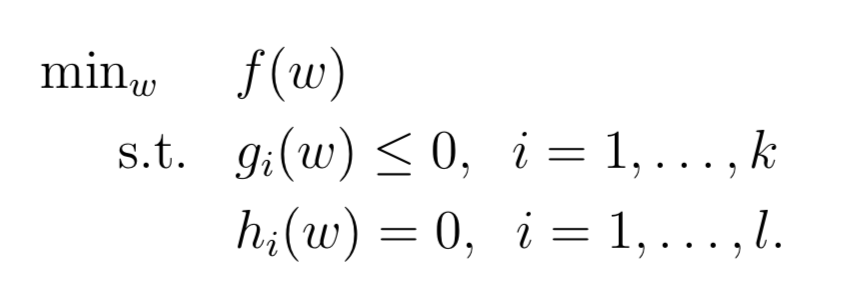
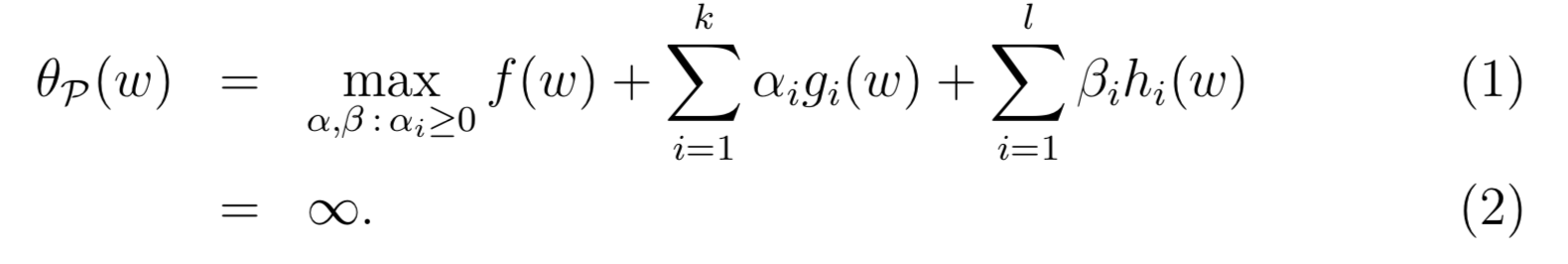
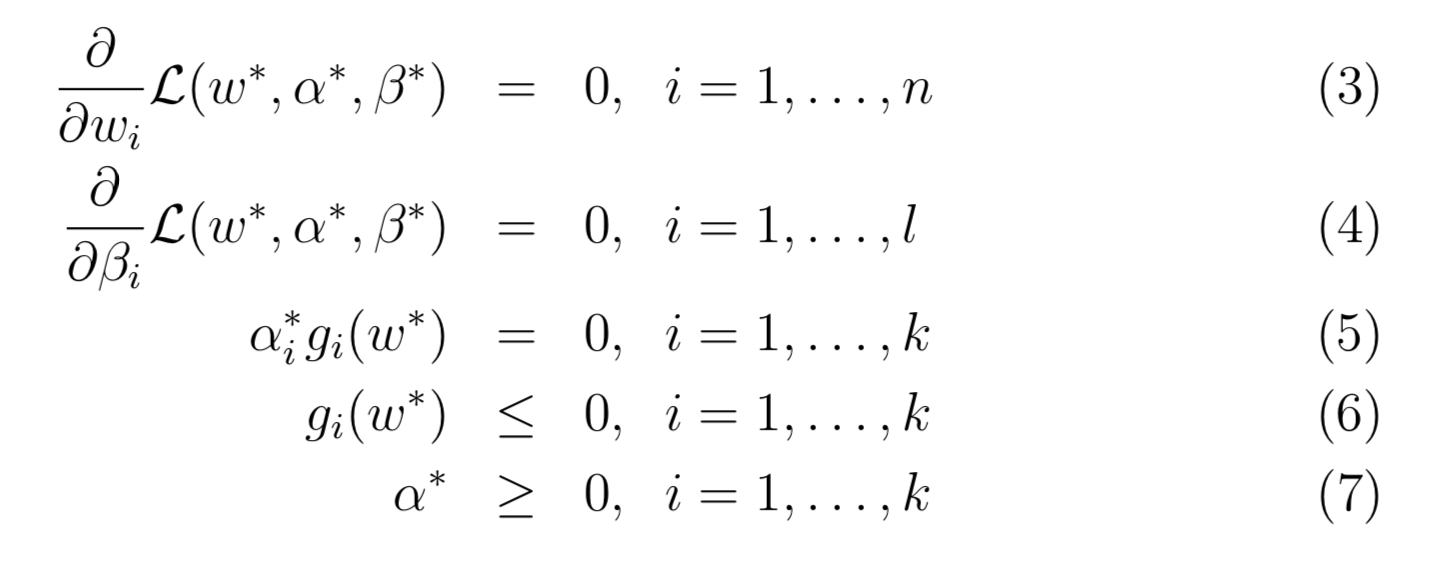
预览: