cs229 笔记 4:生成学习算法
前面讲到的学习算法都是对
和判别学习算法不同的是,生成学习算法对
举个栗子,假如我们想判断一个动物是大象 (
其中
高斯判别分析
首先介绍高斯判别分析 GDA (Gaussian discriminant analysis),它假定
多维正态分布
n 维正态分布 (又叫高斯分布),它的参数包括一个均值向量
其中
假设随机变量
假设随机变量
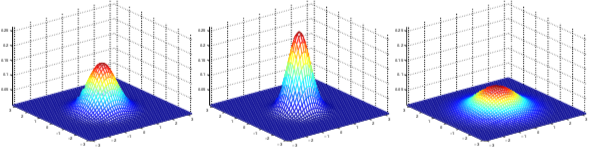
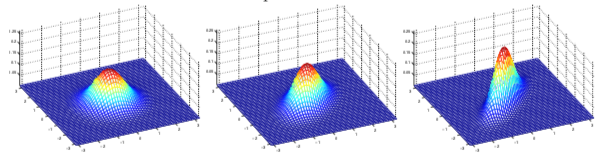
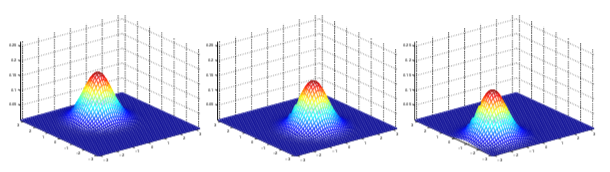
如下是几个二维高斯分布的概率密度图形示例
左边图形:均值为零向量 (2X1 的零向量),协方差矩阵
均值都为 0,协方差矩阵如下
固定
高斯判别分析模型
使用多维正态分布对
对应的概率密度
这里的参数为:
通过最大化
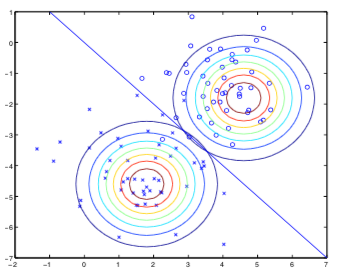
该算法的执行情况如下图所示:这里有两个正态分布,它们有相同的协方差矩阵和不同的期望值,分别对应训练集中的两种分类。图中的直线表示预测的分界线 (
GDA 和逻辑回归
如果将
其中
事实上,如果
朴素贝叶斯
和 GDA 不同的是,朴素贝叶斯算法中
考虑使用多项分布模型表示
贝叶斯假设:给定
第一个等式可根据条件概率性质推导,证明两边相等只需要在等式两边分别乘以
我们的模型参数是:
最大似然估计如下
对于新的样本,可以通过下式计算它的后验概率
拉普拉斯平滑
在使用朴素贝叶斯算法对新的邮件进行分类时,假设 “nips” 表示词典中第 35000 个单词,它在之前的样本中从未出现过,那么最大似然估计的参数
因为没有见过 “nips” 这个单词,导致两种类型概率均为 0。后验概率的计算结果为
考虑预估多项分布随机变量
对该式应用拉普拉斯平滑可得
回到邮件分类问题,应用拉普拉斯平滑后,条件概率的分子不再为 0
文本分类事件模型
前面讨论的贝叶斯分类模式是多元伯努利事件模型 (multi-variate Bernoulli event model),在该模型中,我们假定邮件的生成方式如下
- 随机决定发送垃圾邮件或非垃圾邮件 (
- 根据
这样最终发送邮件的概率可表示为
多项式事件模型
使用
- 随机决定发送垃圾邮件或非垃圾邮件 (
- 然后根据多项式分布模型选择
- 再通用根据多项式分布模型独立于
- 依次选择其他单词,直到选完 n 个单词
最终邮件的概率可表示为
在该模型中
给定训练集 {
最大似然估计如下
应用拉普拉斯平滑后结果如下
- 2018-07-07
二分类 (binary classification) 是最简单的一种分类问题,
- 2018-07-05
俗话说好记性不如烂笔头,看过的东西很快就会忘了,记录下来一方面会增强记忆,另一方面也方便查阅。这里根据 css229 视频和讲义简单做下笔记。
- 2018-07-08
前两节分别介绍了一个回归模型和一个分类模型,其中线性回归中假设概率分布为
- 2018-05-20
升级了 theme-next 主题,开启了 Mathjax 功能,测试下书写公式,先来个看看
- 2018-08-04
感知机算法是 <统计学习方法> 这本书讲的第一个机器学习算法,据说是最简单的机器学习算法。这里参考书中的例子,使用程序实现该算法,以便加深理解。

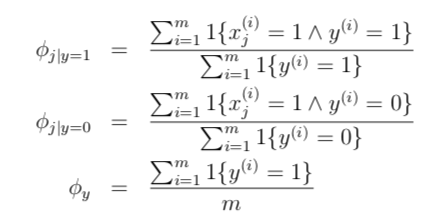
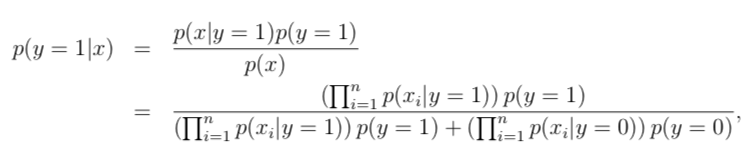
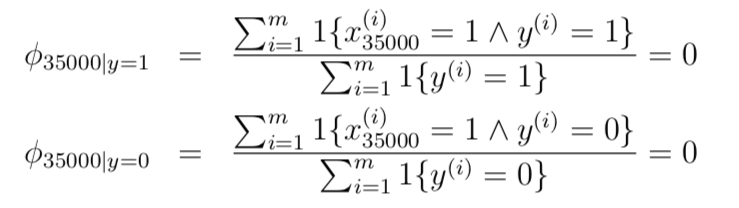
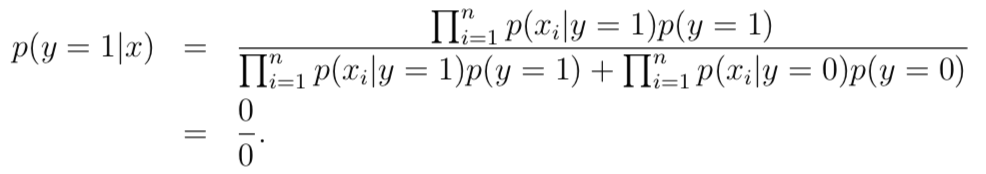
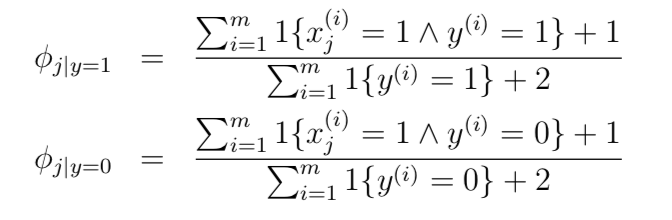
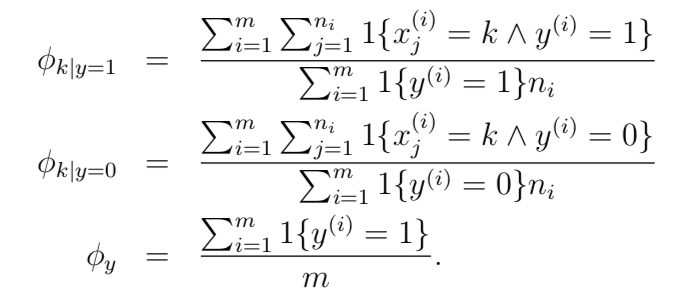
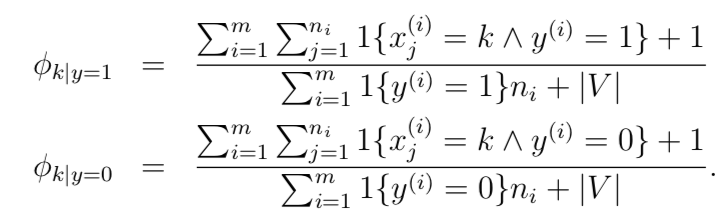
预览: