cs229 笔记 3:广义线性模型
前两节分别介绍了一个回归模型和一个分类模型,其中线性回归中假设概率分布为
指数分布族
在讲广义线性模型之前先介绍下指数族分布,指数族分布是指概率分布可以写如下形式的分布
其中
给定 T、a、b 的定义,可以得到一族以
伯努利分布
均值为
可以将其概率写成如下形式
令自然参数
高斯分布
根据之前线性回归 概率解释 的推导过程可知,
令 T、a、b、
还有很多其他的分布也属于指数族分布,比如多项式分布、泊松分布、伽马分布、指数分布、beta 分布、Dirichlet 分布等
构造 GLMs
广义线性模型基于指数族分布。为了构造广义线性模型,首先给出关于条件概率分布
给定
自然参数
最小二乘法
最小二乘法 (Ordinary Least Squares) 是 GLM 的一种特殊情况。目标变量
根据假设
逻辑回归
目标变量取值范围为
引入
Softmax Regression
假设分类问题中,输出变量
使用 k 个参数
定义
引入指示函数 I {.},如果括号内取值为 True 则结果为 1 (I {True} = 1),否则结果为 0 (I {False} = 0)。T (y) 和 y 之间的关系可以表示为
因此
link function 可表示为
为方便表示,定义
可以得到
因此
这个函数将
根据假设 3,
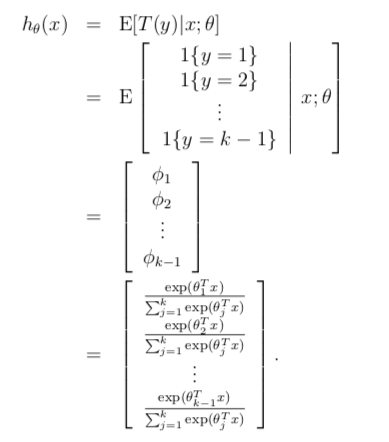
该模型用于解决多分类问题,叫做 softmax regression,它是逻辑回归的一般化。这里学习函数的输出如下
对
根据以上结论,可以得到 log 似然函数如下。据此可以求出最大似然估计值 (可以使用梯度上升或牛顿方法)
- 2018-07-07
二分类 (binary classification) 是最简单的一种分类问题,
- 2018-07-05
俗话说好记性不如烂笔头,看过的东西很快就会忘了,记录下来一方面会增强记忆,另一方面也方便查阅。这里根据 css229 视频和讲义简单做下笔记。
- 2018-07-19
本节首先介绍函数间隔和几何间隔的概念,进而引出最优间隔分类器和拉格朗日对偶,最后介绍核函数和 SMO algorithm
- 2018-07-14
前面讲到的学习算法都是对
- 2018-05-20
升级了 theme-next 主题,开启了 Mathjax 功能,测试下书写公式,先来个看看

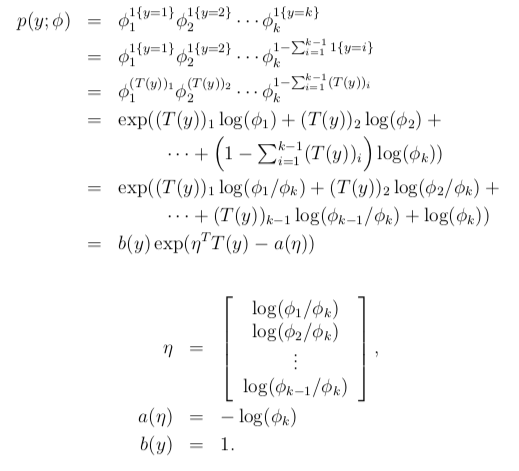
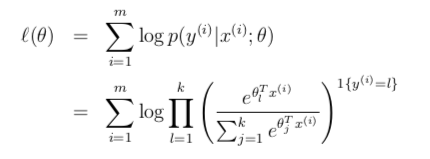
预览: